6 Lineare Regression
- Korrelation
- Lineare Regression
6.1 Übungen
Übung 6.1 Wann darf man den Pearson’sche Korrelationskoeffizient verwenden?
Übung 6.2 Welche Alternativen gibt es zum Pearson’sche Korrelationskoeffizient?
Übung 6.3 Was beschreibt das Bestimmtheitsmaß?
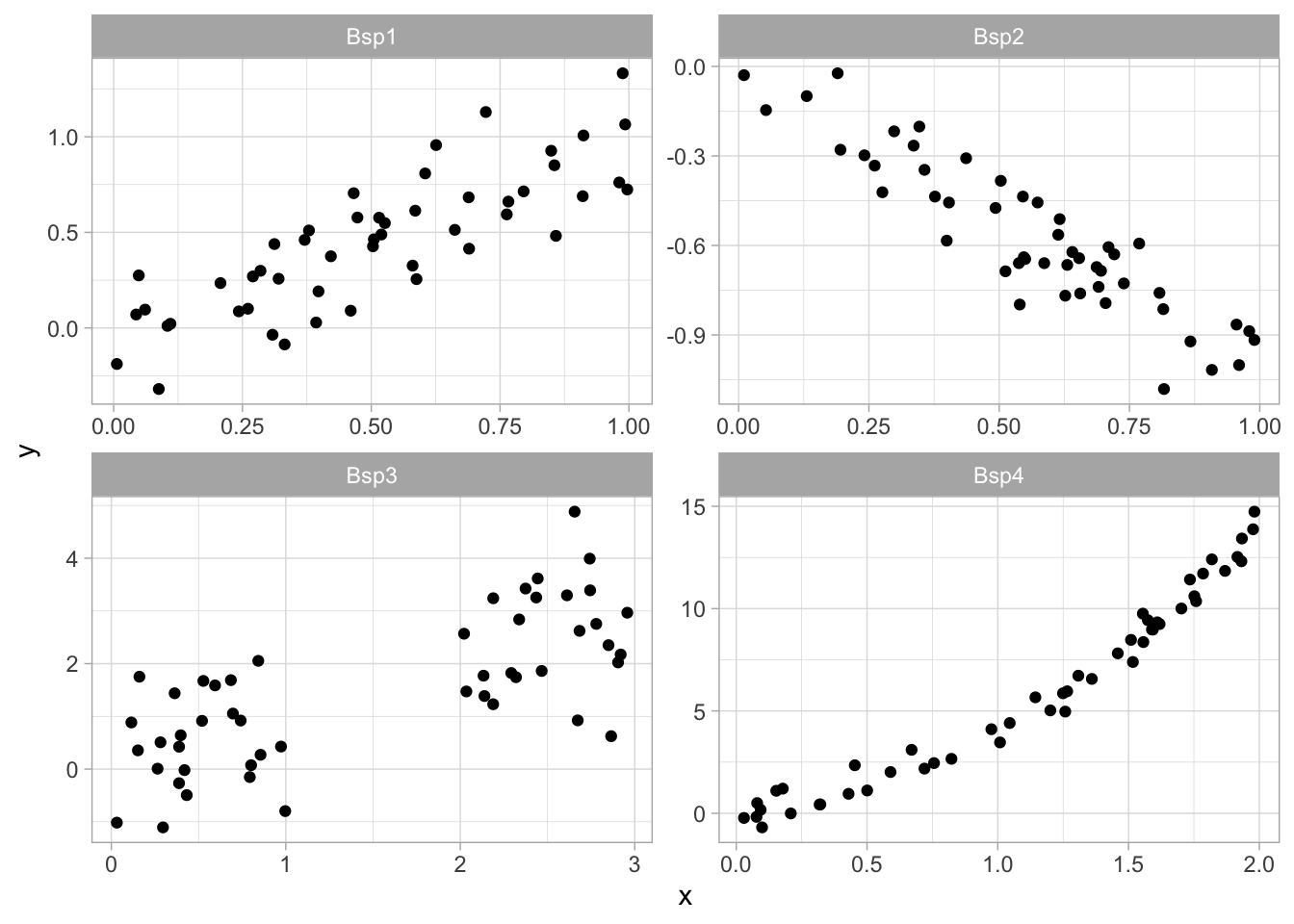
Übung 6.4 In den vier Scatterplots ist der Zusammenhang zwischen jeweils zwei Variablen dargestellt.
- Geben Sie an, für welchen Zusammenhang (Bsp1 - Bsp4) Sie den Pearsonschen Korrelationskoeffizienten für einen linearen Zusammenhang berechnen dürfen.
- Falls Sie diesen berechnen dürfen, schätzen Sie diesen ab und tragen ihn in die Grafik ein.
- Falls Sie diesen nicht berechnen dürfen, erklären Sie warum und geben Sie an ob es eventuell eine Alternative gib.
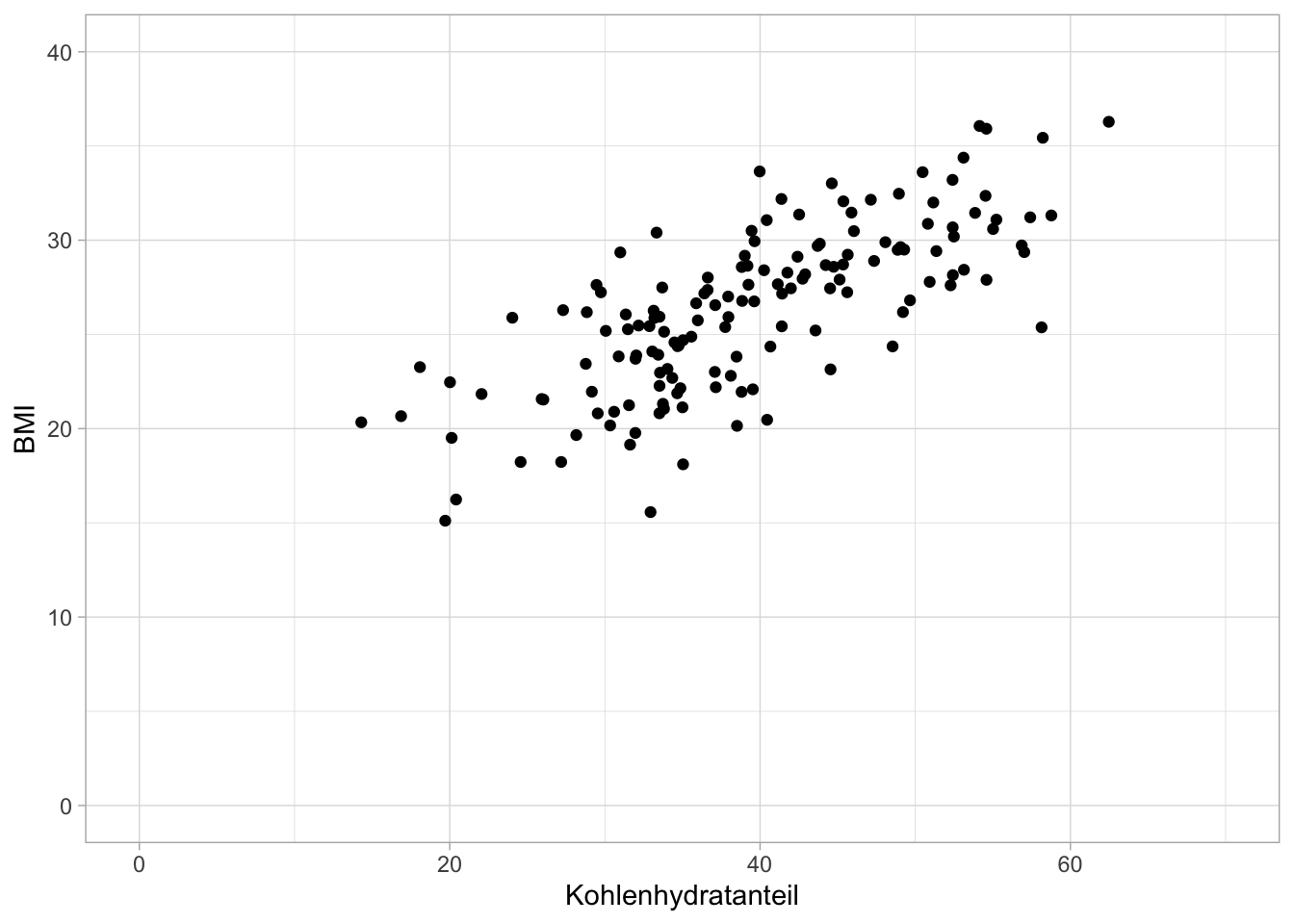
Übung 6.5 Bei 150 Personen wird der mittlere Kohlenhydratanteil (in \(\%\)) in der Nahrung von einer Woche gemessen und der BMI. Es stellt sich die Frage, ob es einen linearen Zusammenhang zwischen diesen beiden Merkmalen gibt. Kann anhand des Anteils der Kohlenhydrate in der Nahrung auf den BMI geschlossen werden? Um dies zu beantworten wird eine lineare Regression berechnet, wobei die Zielgröße der BMI ist und die unabhängige Variable der Anteil der Kohlenhydrate in der Nahrung. Der Output der linearen Regression aus R ist unten angeführt:
- Wie schaut der funktionale Zusammenhang aus und welchen mittleren BMI kann ich bei einem Anteil von \(40\%\) Kohlenhydrate in der Nahrung erwarten.
- Welchen Anteil der Variabilität des BMI kann durch das Modell erklärt werden, ist das ihrer Meinung nach gut?
- Ist der Zusammenhang zwischen BMI und Anteil der Kohlenhydrate signifikant?
- Zeichnen Sie die geschätzte Funktion in der Grafik ein?
Call:
lm(formula = bmi ~ carb, data = dat)
Residuals:
Min 1Q Median 3Q Max
-8.651 -2.370 0.129 1.929 7.111
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 13.37394 0.98938 13.52 <2e-16 ***
carb 0.32926 0.02437 13.51 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.924 on 148 degrees of freedom
Multiple R-squared: 0.5522, Adjusted R-squared: 0.5492
F-statistic: 182.5 on 1 and 148 DF, p-value: < 2.2e-16