[1] "omnivore" "vegan" "vegetarisch" "vegetarisch" "pescetarisch"
[6] "vegetarisch" "pescetarisch" "omnivore" "vegan" "omnivore"
[11] "pescetarisch" "omnivore" "pescetarisch" "pescetarisch" "vegetarisch"
[16] "vegetarisch" "vegan" "pescetarisch" "omnivore" "vegan"
[21] "vegan" "pescetarisch" "omnivore" "vegetarisch" "omnivore"
[26] "vegetarisch" "vegetarisch" "pescetarisch" "pescetarisch" "vegetarisch"
[31] "omnivore" "vegan" "pescetarisch" "omnivore" "vegetarisch"
[36] "vegetarisch" "vegan" "omnivore" "omnivore" "omnivore"
[41] "omnivore" "omnivore" "vegetarisch" "pescetarisch" "pescetarisch"
[46] "vegetarisch" "pescetarisch" "pescetarisch" "vegetarisch" "vegetarisch" 1 Deskriptive Statistik
In der deskriptiven Statistik geht es darum, die Daten anhand von Kennzahlen und Grafiken zu beschreiben beziehungsweise zu charakterisieren. Welche Kennzahlen und Grafiken sinnvoll sind, ist vom Datentyp abhängig.
1.1 Datentypen
Im wesentlichen unterscheidet man zwischen drei Datentypen:
- Nominal skalierte Daten
- Ordinal skalierte Daten
- Metrisch skalierte Daten
1.1.1 Nominal skalierte Daten
Nominal skalierte Daten sind Daten, die eine bestimmte Anzahl von verschiedenen Ausprägungen haben kann. Für diese Ausprägungen ist nur Gleichheit und Ungleichheit definiert. Also entweder sind zwei Ausprägungen gleich oder eben unterschiedlich. Beispiele dafür sind Geschlecht, Farben, Herkunftsland und ähnliches. Als mathematische Operatoren sind nur \(=\) und \(\neq\) definiert. In der Statistik ist es oft üblich diese Ausprägungen anhand natürlichen Zahlen zu codieren. Existieren nur zwei Ausprägungen, wie zum Beispiel Gewinn und Verlust, dann spricht man von einem dichotomen Merkmal. Bei dichotomen Merkmalen werden die Ausprägungen in der Regel mit 0 und 1 codiert.
Beispiel 1.1 (Nominal skalierte Daten) Ein paar Beispiele für nominal skalierte Daten:
- Gesundheitszustand: gesund, krank (dichotom)
- Geschlecht: weiblich, männlich, divers
- Ernährungstyp: Omnivor:in, Pescetarier:in, Vegetarier:in, Veganer:in, …
1.1.2 Ordinal skalierte Daten
Ordinal skalierte Daten haben wie nominal skalierte Daten nur eine bestimmte Anzahl von Ausprägungen. Zusätzlich gibt es eine Reihenfolge oder Rangordnung zwischen den Ausprägungen. Es ist klar definiert, welche Ausprägung kleiner, niedriger, schlechter ist als eine andere. Somit sind auch die mathematischen Operatoren \(<\) und \(>\) definiert.
Beispiel 1.2 (Ordinal skalierte Daten) Ein paar Beispiele für ordinal skalierte Daten:
- Schulnoten: sehr gut, gut, …, nicht genügend (oder 1, 2, 3, 4, 5)
- Bildungsgrad: Hauptschule, AHS, Studium, …
- Qualitätsstufen: 1, 2, 3, 4, 5
- Bewertung: 0 bis 5 Sterne
1.1.3 Metrisch skalierte Daten
Metrische Daten sind Daten, die man im herkömmlichen Sinne messen oder abzählen kann. Man unterscheidet zwischen diskreten und stetigen Daten. Diskrete Daten sind Daten die man abzählen kann oder anhand von natürlichen Zahlen beschreiben kann. Stetige Daten sind Daten, die in einem beliebig großem Intervall theoretisch unendlich viele Werte annehmen können Der Unterschied zu ordinalen Daten ist, dass man ein Verhältnis bilden kann, so sind 10 Meter doppelt so lange wie 5 Meter. Im Gegenzug dazu kann man nicht sagen, dass bei den Schulnoten eine 2 doppelt so schlecht ist wie eine 1, weil dann müsste 4 doppelt so schlecht sein wie eine 2, wobei aber die 3 noch dazwischen liegt. Das ist darauf zurück zu führen, dass bei ordinalen Daten kein Abstand zwischen den einzelnen Ausprägungen definiert ist, sondern nur die Reihenfolge.
Beispiel 1.3 (metrisch skalierte Daten) Ein paar Beispiele für diskrete metrisch skalierte Daten:
- Anzahl der verdorbenen Erdbeeren in eine Kiste: 0, 1, 2, 3,…
- Alter in Jahren: 18, 19, 20, …
Ein paar Beispiele für stetige metrisch skalierte Daten:
- BMI von Personen
- Blutzuckerspiegel
- Aflatoxingehalt in einer Nusspackung
1.2 Nominal skalierte Daten
Wie in Section 1.1.1 kurz beschreiben sind bei nominal skalierten Daten nur Gleichheit und Ungleichheit definiert. Daher bietet sich für eine Zusammenfassung der Daten die Häufigkeiten, wie oft die einzelnen Ausprägungen beobachtet wurden, an.
1.2.1 Häufigkeiten
Angenommen die beobachteten Daten haben \(m\) verschieden Ausprägungen und \(j=1,2,\ldots , m\) ist der dazugehörige Index.
Definition 1.1 (Absolute Häufigkeit) Die absoluten Häufigkeiten \(H_j\) sind defniert, als die Anzahl wie oft die \(j\)-te Ausprägung beobachtet wurde. Der Stichprobenumfang ist dann gegeben durch die Summe aller \(m\) absoluten Häufigkeiten \(H_j\), also definiert durch
\[ n=\sum_{j=1}^m H_j. \]
Beispiel 1.4 (Ernährungsweise) Es wurden \(n=50\) Personen bezüglich ihrer Ernährungsweise befragt, dabei konnten diese aus den folgenden \(m=4\) Kategorien wählen: omnivore, pescetarisch, vegetarisch und vegan. Es wurden folgende Werte beobachtet:
Daraus ergeben sich folgenden absolute Häufigkeiten:
| Ernährungsweise | absolute Häufigkeiten |
|---|---|
| omnivore | 14 |
| pescetarisch | 14 |
| vegan | 7 |
| vegetarisch | 15 |
Bei einem Vergleich von zwei Stichproben mit unterschiedlichen Stichprobenumfang ist es oft nicht einfach, die Unterschiede zwischen den beiden Stichproben anhand der absoluten Häufigkeiten zu erkennen. Ein Vergleich ist um vieles einfacher, wenn man relative Häufigkeiten betrachtet.
Definition 1.2 (Relative Häufigkeit) Die relativen Häufigkeiten sind defniert durch \(h_j=H_j/n\) und es gilt
\[ \sum_{j=1}^m h_j=1. \]
Die Summe aller relativen Häufigkeiten ist somit \(1\). Die relativen Häufigkeiten werden auch gerne in Prozentwerten ausgedrückt.
Beispiel 1.5 (Fortsertzung Ernärungsweisen) Angenommen bei den \(25\) Personen weiß man auch noch das Geschlecht und möchte die Verteilung der Ernährungsweisen zwischen den beiden Geschlechtern vergeleichen. Die absoluten Häufigkeiten sind in der Tabelle 1.1 aufgelistet.
| Ernährungsweise | Geschlecht | absolute Häufigkeiten |
|---|---|---|
| omnivore | männlich | 2 |
| omnivore | weiblich | 12 |
| pescetarisch | männlich | 3 |
| pescetarisch | weiblich | 11 |
| vegan | männlich | 1 |
| vegan | weiblich | 6 |
| vegetarisch | männlich | 3 |
| vegetarisch | weiblich | 12 |
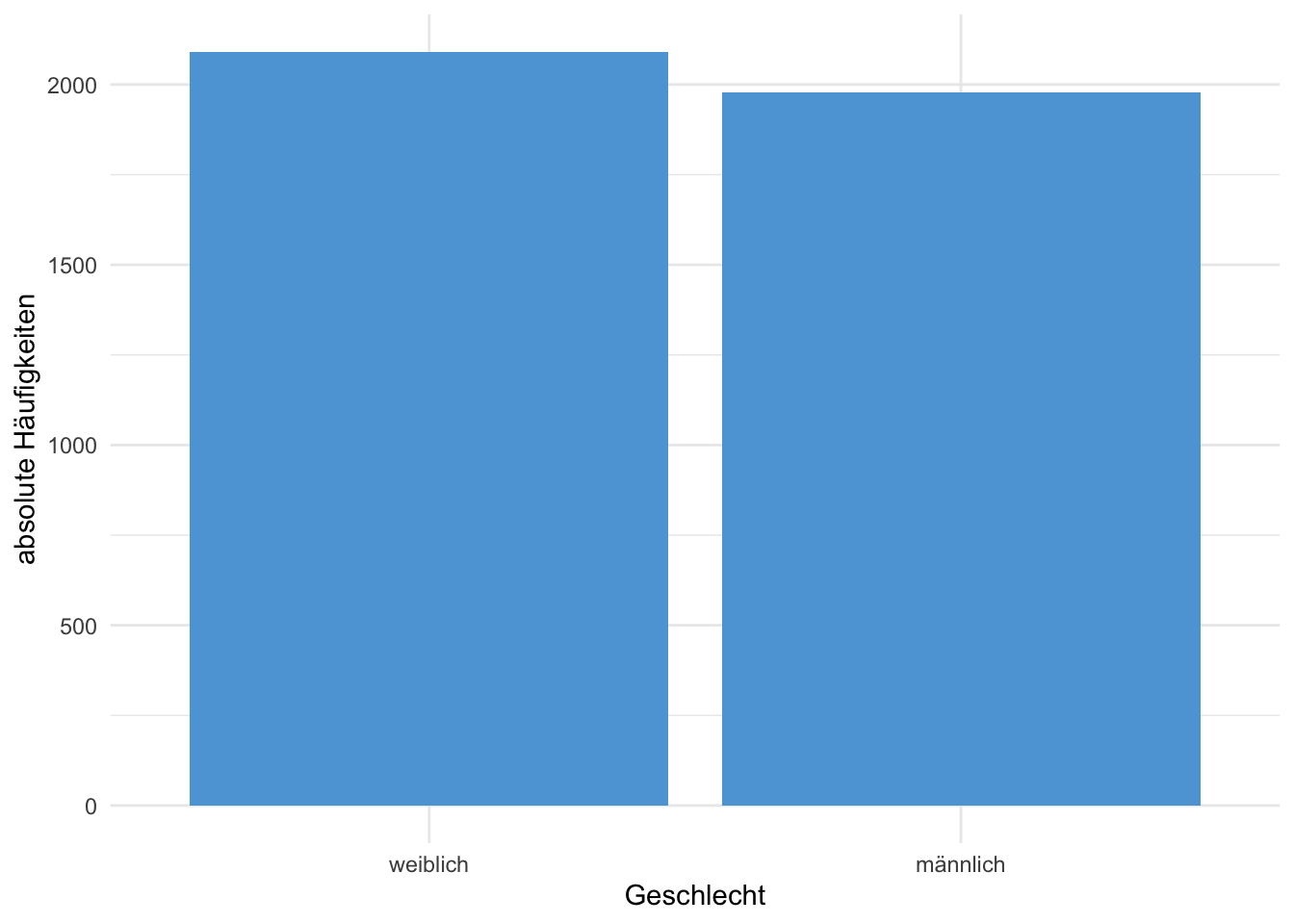
Beispiel 1.6 (Häufigkeiten Geschlecht NHANES Daten) In der Tabelle 1.2 sind die absoluten und relativen Häufigkeiten der weiblichen und männlichen Personen im NHANES Datensatz aufgelistet. In der Abbildung 1.1 sind die absoluten Häufigkeiten als Balkendiagramm dargestellt.
| Geschlecht | absolut | relativ |
|---|---|---|
| weiblich | 2091 | 0.514 |
| männlich | 1978 | 0.486 |
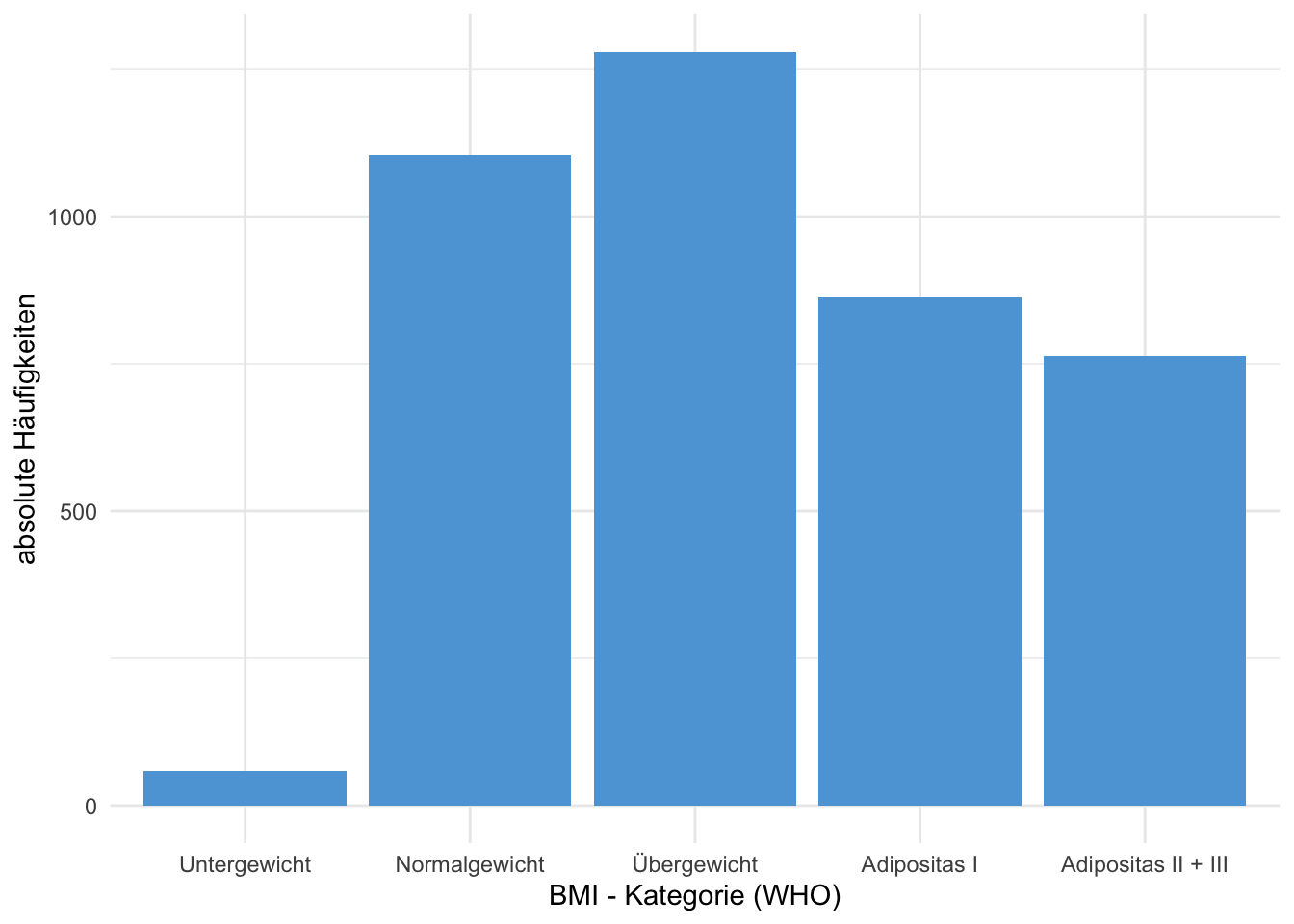
Beispiel 1.7 (Häufigkeiten BMI Kategorien laut WHO in NHANES Daten) In der Tabelle 1.3 sind die absoluten und relativen Häufigkeiten der BMI-Kategorien im NHANES Datensatz aufgelistet. In der Abbildung 1.2 sind die absoluten Häufigkeiten als Balkendiagramm dargestellt.
| BMI-Kategorie | absolut | relativ |
|---|---|---|
| Untergewicht | 59 | 0.014 |
| Normalgewicht | 1104 | 0.271 |
| Übergewicht | 1280 | 0.315 |
| Adipositas I | 863 | 0.212 |
| Adipositas II + III | 763 | 0.188 |
Pivot-Tabelle
- Häufigkeitsverteilung zweier Merkmale
- Geschlecht
- BMI-Kategorie
| weiblich | männlich | |
|---|---|---|
| Untergewicht | 35 | 24 |
| Normalgewicht | 562 | 542 |
| Übergewicht | 581 | 699 |
| Adipositas I | 438 | 425 |
| Adipositas II + III | 475 | 288 |
Relative Häufigkeiten
- bezogen auf das Geschlecht
| weiblich | männlich | |
|---|---|---|
| Untergewicht | 1.7 | 1.2 |
| Normalgewicht | 26.9 | 27.4 |
| Übergewicht | 27.8 | 35.3 |
| Adipositas I | 20.9 | 21.5 |
| Adipositas II + III | 22.7 | 14.6 |
- 27.8 % der Frauen haben einen BMI \(> 25\) und \(\leq 30\)
Relative Häufigkeiten bezogen auf den BMI
| weiblich | männlich | |
|---|---|---|
| Untergewicht | 59.3 | 40.7 |
| Normalgewicht | 50.9 | 49.1 |
| Übergewicht | 45.4 | 54.6 |
| Adipositas I | 50.8 | 49.2 |
| Adipositas II + III | 62.3 | 37.7 |
Bei den Personen in der Gruppe \((25,30]\) sind 54.6% männlich
1.3 Metrisch skalierte Daten
Ein wesentlicher Aspekt in der Statistik ist es anhand einer Stichprobe Rückschlüsse auf die Grundgesamtheit zu machen. Wie schon erwähnt spielen dabei Grafiken und Kennzahlen eine wichtige Rolle. Zwei beliebte grafische Darstellungen sind das Histogramm und der Boxplot. Die Kennzahlen teilt man in drei Gruppen ein, je nachdem welchen Aspekt der Daten sie beschreiben: das Zentrum und die Lokation, die Variabilität und die Form einer Verteilung.
1.3.1 Histogramm
Für das Histogramm teilt man den Wertebereich der Daten in Klassen ein, und betrachtet die Anzahl der Werte die in die jeweilige Klasse fallen. Für jede Klasse wird nun eine Balken gezeichnet, der so hoch ist, dass die Fläche des Balken die Anzahl der Werte widerspiegelt. Da die Berechnung der Fläche etwas umständlich ist, nimmt man in der Regel gleich große Klassen und trägt pro Klasse als Höhe die Anzahl der Werte pro Klasse auf. Da bei der Klasseneinteilung die Klassen direkt aneinander liegen, gibt es im Gegensatz zum Balkendiagramm keinen Abstand zwischen den Balken.

Anzahl der Klassen
Es stellt sich die Frage, wie viele Klassen sollen gemacht werden, beziehungsweise wie groß soll die Klassenbreite sein. Dafür gibt es keine exakte Vorschrift aber eine Faustregel. Diese Fasutregel besagt, dass die Anzahl der Klassen circa \(\sqrt{n}\) betragen soll. Allgemein gilt, dass es nicht weniger als 5 Klassen sein sollen und nicht mehr als 20. Bei einer sehr großen Stichprobe (\(n > 1000\)) kann die Klassenanzahl auch größer als 20 sein. Die Wahl der Klassenbreite kann das Erscheinungsbild des Histogramms stark beeinflussen, daher ist es sinnvoll immer verschiedene Klassenbreiten/anzahl auszuprobieren und jene zu wählen, bei der die Form der Verteilung gut ersichtlich ist.
1.4 Kennzahlen
1.4.1 Zentrum
Arithmetisches Mittel
Das arithmetische Mittel ist wohl die bekannteste statistische Kennzahl. Es ist definiert als die Summe aller Werte dividiert durch die Anzahl der Werte.
Definition 1.3 (Arithmethisches Mittel) \[ \bar{x}=\frac{x_1 + x_2 + \ldots + x_n}{n}=\frac{1}{n}\sum_{i=1}^n x_i \]
Eigenschaften des arithm. Mittel
- empfindlich gegenüber Ausreißer
- ungeeignet bei mehr-gipfeligen oder schiefen Verteilungen
- bei diskreten Werten muss das berechnete \(\bar{x}\) nicht unbedingt auftreten.
Beispiel 1.8 (Arithmetisches Mittel) Gegeben sei eine Stichprobe der Größe \(n=\) 10 mit folgende Werten:
[1] 5.3 10.2 6.7 8.1 7.6 6.2 8.5 8.3 7.9 11.2Sie Summe dieser Werte ist 80. Dividiert man diese durch den Stichprobenumfang \(n=\) 10 so ergibt sich ein arithm. Mittel \(\bar{x}=\) 8.
Ändert man den letzten Wert von 11.2 zu einem Ausreisser mit einem Wert von 31.2, dann ändert sich die Summe auf 100 und somit auch das arithm. Mittel auf 10. Man erkennt, dass nur ein einziger Wert, der weit weg von den restlichen Werten liegt, das arithm. Mittel stark verändern kann.
Median
Definition 1.4 (Median) Teilt die geordnete Stichprobe in zwei gleich große Teile, d.h. \(50\%\) der Werte sind kleiner gleich dem Median und \(50\%\) der Werte sind größer gleich dem Median.
Eigenschaften des Median
- Robust gegenüber Ausreißer
- nicht sinnvoll bei mehr-gipfeligen Verteilungen
- kann bei nicht allzu schiefen Verteilungen verwendet werden.
- teilt die Stichprobe in zwei gleich große Teile.
Beispiel 1.9 (Median) Bei diesem Beispiel werden die gleichen Daten wie beim arithmetischen Mittel verwendet. Für die Berechnung des Median macht es Sinn die Daten zuerst aufsteigen zu sortieren.
[1] 5.3 6.2 6.7 7.6 7.9 8.1 8.3 8.5 10.2 11.2Da der Stichprobenumfang \(n=\) 10 eine gerade Zahl ist, ist der Median der mittlere Wert zwischen den 5 und 6 Wert. Also die Hälfte von der Summe von 7.9 und 8.1. Somit ist der Median 8. Betrachtet man die zweite Stichprobe mit dem Ausreisser:
[1] 5.3 6.2 6.7 7.6 7.9 8.1 8.3 8.5 10.2 31.2so erkennt man bei der sortierten Stichprobe, dass sich hier der 5 und 6 Wert nicht ändert und somit der Median der gleiche ist wie ohne Ausreisser.
Modalwert
Definition 1.5 (Modalwert) Der Modalwert ist jener Wert eine Stichprobe, der am häufigsten beobachtet wurde.
- direkt verwendbar:
- bei diskreten Werten mit deutlich weniger Ausprägungen als der Stichprobenumfang.
- stetig oder sehr (unendlich) viele Ausprägungen:
- Klasseneinteilung des Beobachtungsraumes
- Modalwert \(=\) Mittelwert der Klassegrenzen der Klasse, in der die meisten Werte liegen.
- Abhängig von der Wahl der Klasseneinteilung
1.4.2 Lage
Lagekennzahlen werden auch als Ordnungsstatistiken bezeichnet. Sie geben an, wie viel Prozent der Werte kleiner als ein vorgegebener Wert sind. Dabei wird nicht der Wert selbst vorgegeben, sondern der Prozentwert \(\alpha\) wird fixiert und dann das dazugehörige Wert aus der Stichprobe berechnet. Dieser wird dann als \(\alpha\)-Quantil bezeichnet. Der Median ist ebenfalls ein Quantil, nämlich das \(50\)%-Quantil, da \(50\)% der Werte kleiner oder gleich dem Median sind.
Quartile
Die Quartile sind spezielle Quantile, aus dem Namen lässt sich ableiten, das diese Quantile die Daten in 4 (Quarter) Bereiche aufteilt. In jedem Bereich befinden sich \(25\)% der Daten, daher sind die verwendeten Prozentsätze: \(25\)%, \(50\)%, und \(75\)%. Das \(25\)%-Quantil (\(Q_{0.25}\)) wird auch das \(1\).Quartil oder unterer Quartil bezeichnet. Das \(75\)%-Quantil (\(Q_{0.75}\)) wird als \(3\). oder obere Quartil bezeichnet.
Quantile
Definition 1.6 (Quantile) Ein \(\alpha\) Quantil ist jener Wert, bei dem \(n\alpha\) Werte kleiner oder gleich diesem Wert sind.
Spezielle Quantile sind die Quartile und Perzentile. Bei den Perzentilen lässt sich \(\alpha\) in der Regel als \(Z/N\) darstellen, wobei \(Z \in \{1, 2, 3, \ldots, 99\}\) ist und \(N=100\).
1.4.3 Streuung
Varianz, Standardabweichung
Definition 1.7 (Varianz) \[ s^2=\frac{1}{n-1}\sum_{i=1}^n (x_i- \bar{x})^2 \]
Definition 1.8 (Standardabweichung) \[ s=\sqrt{s^2} \]
Interquartilsrange
Definition 1.9 (Interquartilsrange) \[ IQR = Q_{0.75} - Q_{0.25} \]
- Robust gegenüber Ausreißer
- \(50\%\) der Werte liegen innerhalb des IQR
- \(IQR/1.349\) … robuster Schätzer für die Standardabweichung
MAD
Definition 1.10 (Median Absolute Deviation (MAD)) \[ MAD = median | x_i - \tilde{x}| \]
- Median der absoluten Abweichungen vom Median der Daten
- Robust gegenüber Ausreißer
- \(1.4826*MAD\) … robuster Schätzer für \(\sigma\)
Spannweite
Definition 1.11 (Spannweite) \[ R = \max(x_i) - \min(x_i) \]
- Stark beeinflusst durch Ausreißer
- nicht geeignet um Stichproben unterschiedlicher Größen zu vergleichen
1.4.4 Form
Schiefe
Definition 1.12 (Schiefe) \[ s_k = \frac {\frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^{3}} {\sqrt{ (\frac{1}{n}\sum_{i=1}^n (x_i - \bar{x})^{2})^{3}}} \]
- \(s_k \approx 0\) … symmetrische Verteilung
- \(s_k > 0\) … rechtsschiefe Verteilung
- \(s_k < 0\) … linksschiefe Verteilung
Kurtosis
Definition 1.13 (Kurtosis) \[ kur= \frac{ \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x})^{4}}{( \frac{1}{n} \sum_{i=1}^n (x_i - \bar{x}^{2})^{2}} -3 \]
- \(kur \approx 0\) … normale Wölbung (wie Normalverteilung)
- \(kur > 0\) … starke Wölbung (steilgipfelig)
- \(kur < 0\) … schwache Wölbung (flachgipfelig)
1.5 Übungen
Kennzahlen
Übung 1.1 Welche Eigenschaften hat das arithm. Mittel?
Übung 1.2 Welche Eigenschaften hat der Median?
Übung 1.3 Wann ist es besser den Median anstatt das arithm. Mittel zu verwenden, um das Zentrum eine Verteilung zu beschreiben?
Übung 1.4 Bei einer Stichprobe von \(n=80\) Personen wurde der BMI gemessen. Das \(Q_{0.25} = 20\), was sagt es aus?
Übung 1.5 Welche Kennzahlen beschreiben die Variabilität der Daten?
Übung 1.6 Mit welchen Kennzahlen kann man die Form einer Verteilung beschreiben?
Visualisierung
Übung 1.7 Wann verwende ich ein Balkendiagramm und wann ein Histogramm? Worin unterscheiden sich diese beiden Grafiktypen?
Übung 1.8 Welche Aspekte gibt es bei der Erstellung eines Histogramms zu beachten?
Übung 1.9 Auf welchen Kennzahlen basiert die Darstellung des Boxplots?
Übung 1.10 Was erkenne ich im Histogramm, aber nicht im Boxplot?
Übung 1.11 Was erkenne ich im Boxplot, aber nicht im Histogramm?
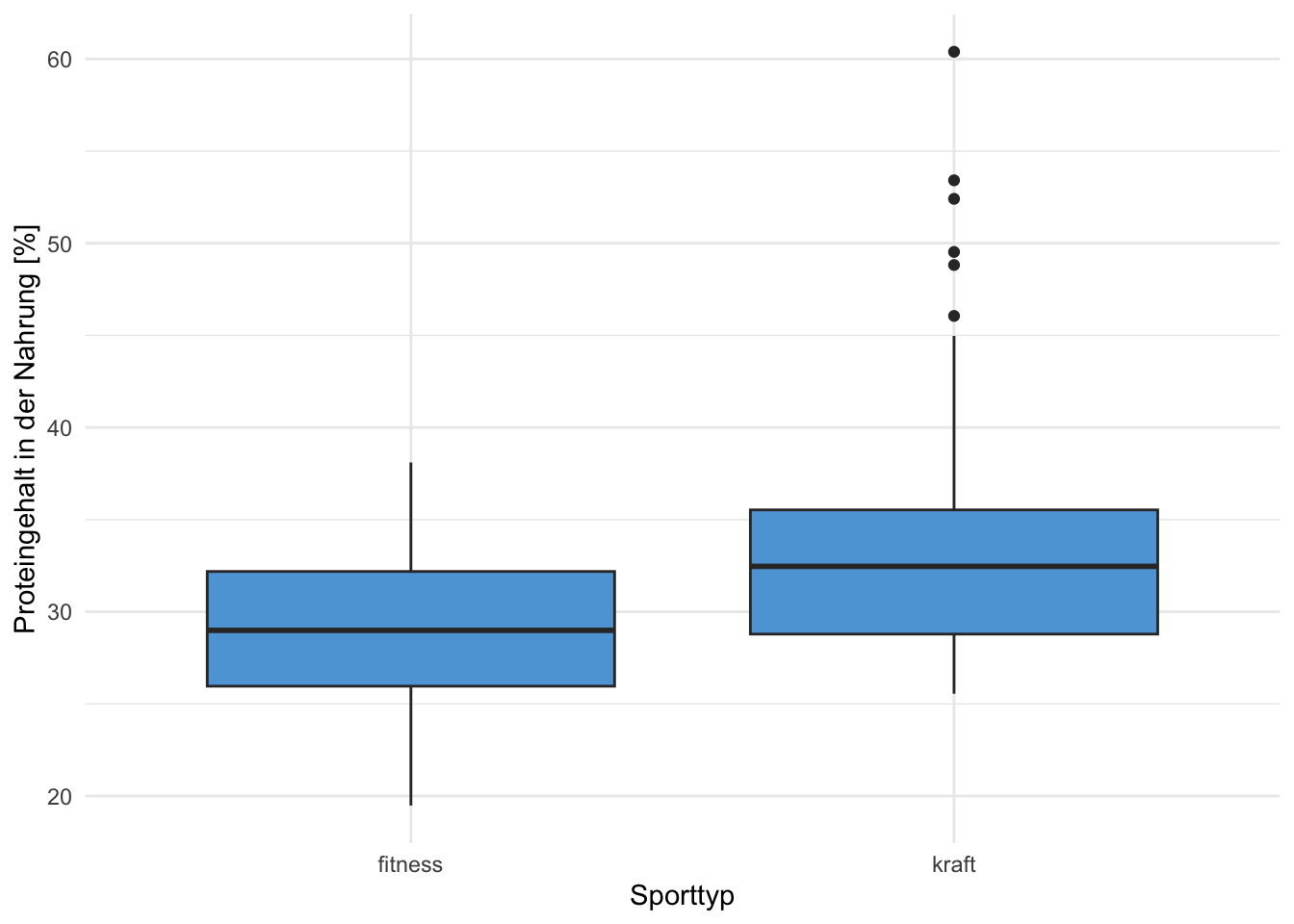
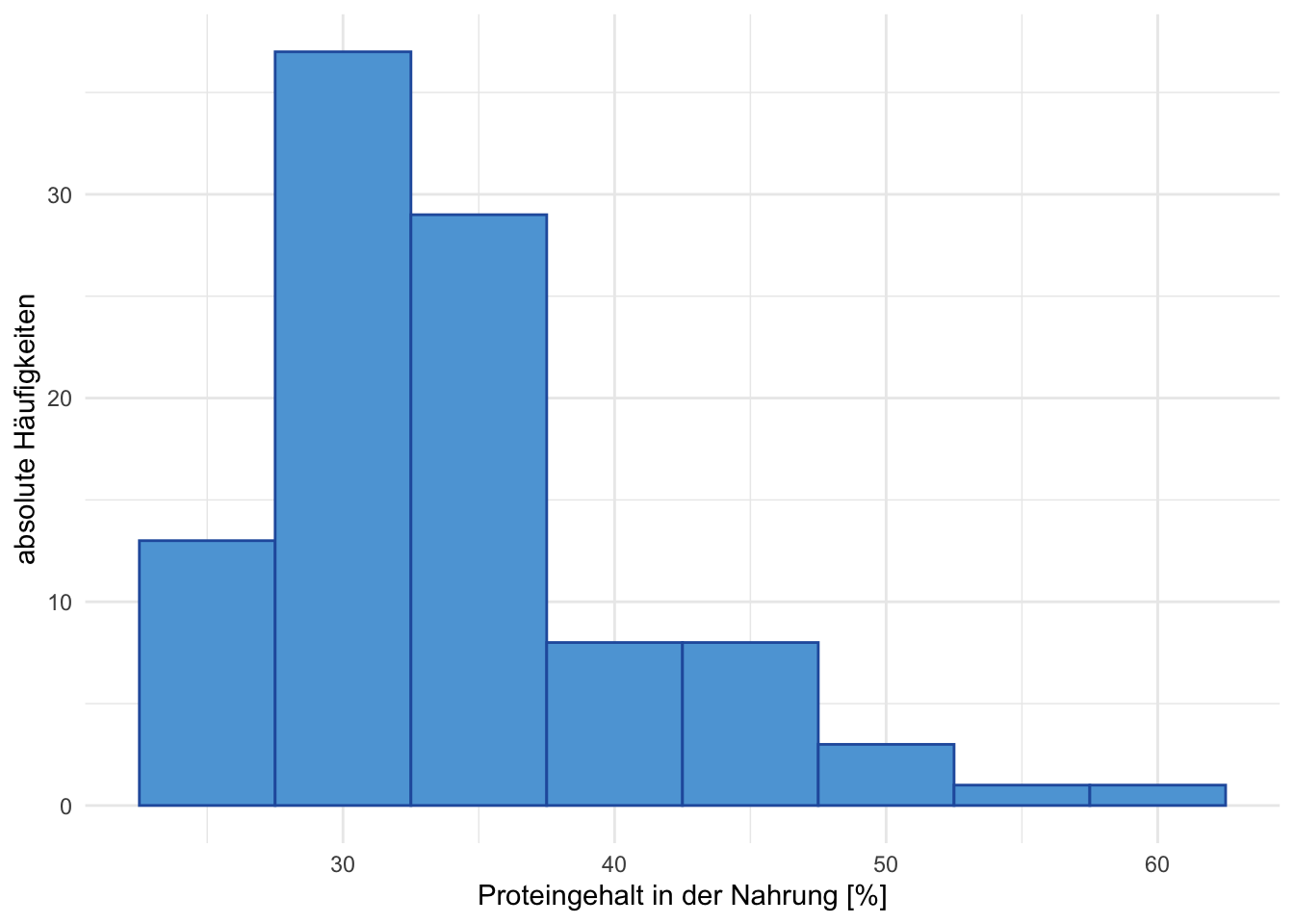
Übung 1.12 Es wurde bei 100 Kraft-Sportler:innen und bei 100 Fitness-Sportler:innen der mittlere Proteingehalt (in %) der Nahrung von einer Woche gemessen. Die Daten sind in den beiden Grafiken A und B dargestellt. Beschreiben Sie alle Aspekte, die Sie aus den beiden Grafiken ablesen und interpretieren Sie diese.
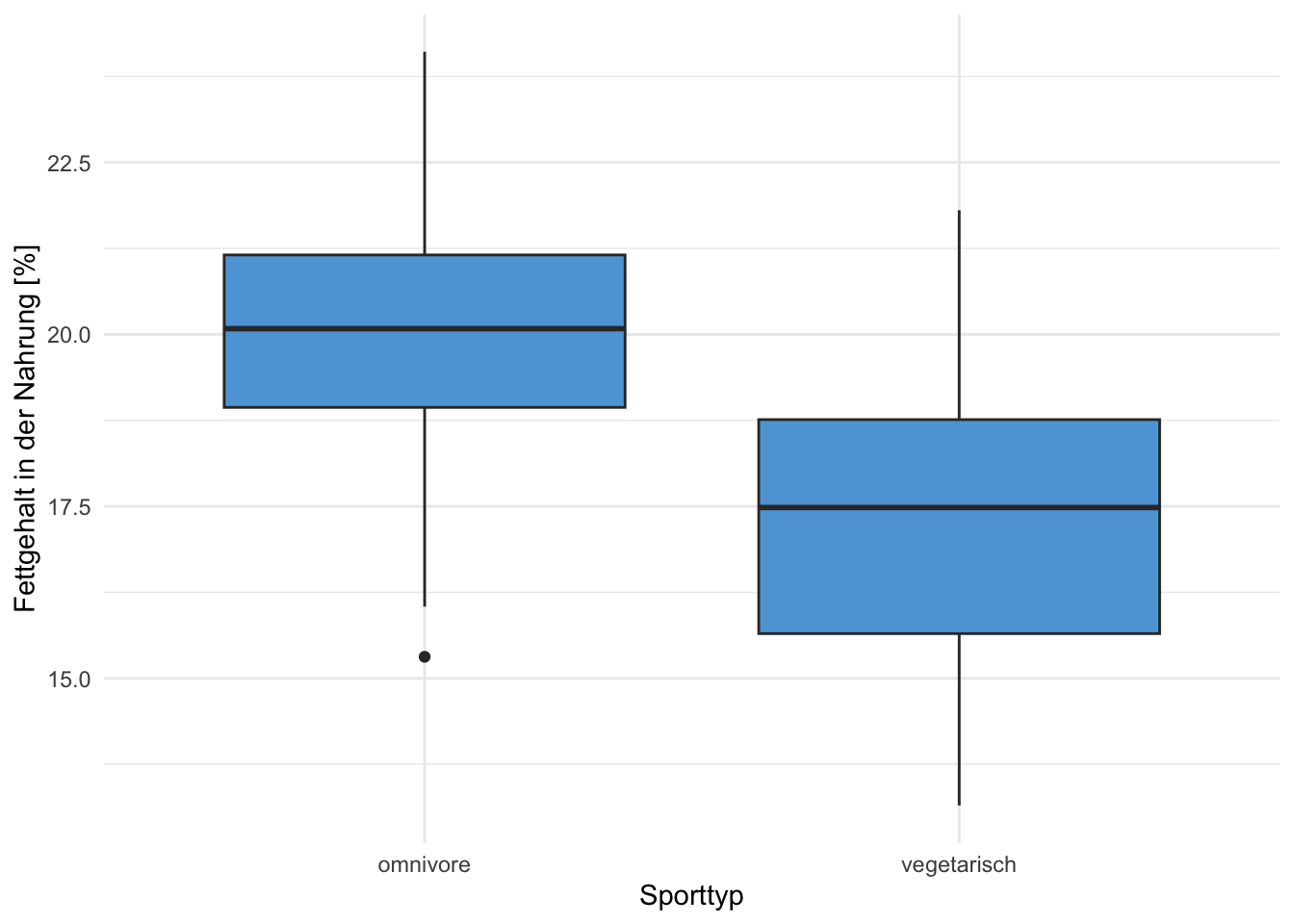
Übung 1.13 Es wurde bei 100 Omnivore und bei 100 Vegetarier der mittlere Fettgehalt (in %) der Nahrung von einer Woche gemessen. Die Daten sind in den beiden Grafiken A und B dargestellt. Beschreiben Sie alle Aspekte, die Sie aus den beiden Grafiken ablesen und interpretieren Sie diese.